A Simple Bloom Filter
It is a probabilistic data structure, that is commonly used to ask question “whether an element is in it or not?”. From my description, it does seems like a job that Set can do, sooo…
Why Should We Use It?
The major advantage of Bloom Filter is space complexity, while other data structures, such as Set and HashTable requires to store the data itself, Bloom Filter does not requires data storing.
When Should We Use It?
Although Bloom filter has major space complexity advantage, yet it can only answer in probabilistic term: whether an item is “possibly in the filter” or “not a chance in the filter”. Because of this characteristic of Bloom filter, you will only want to use it if :
- You need better space complexity.
- You can tolerate false positives.
- You would not need to delete items from the filter. Simple bloom filter cannot support removal operation.
How Should We Implement It?
There are a couple of components to implement the bloom filter.
A Simple Bloom Filter
import sys
import math
# using murmur hashing function because it returns integer
import mmh3
# use bitarray to manage our main data structure
from bitarray import bitarray
class SimpleBloomFilter(object):
def __init__(self, hash_fn, m, fpr):
self._fpr = fpr
self._hash_fn = hash_fn
# size of bitarray that we should construct
self.size = int(-(m * math.log(fpr)) / (math.log(2) ** 2))
# k = how many time should we do the hash
self._k = math.ceil((m/self.size) * math.log(2))
# construct and initialize the bit array
self._bit_array = bitarray(self.size)
self._bit_array.setall(0)
def add(self, item):
for i in range(self._k):
digest = self._hash_fn.hash(item, i) % self.size
# set the bit into 1
self._bit_array[digest] = 1
def is_possibly_exists(self, item):
for i in range(self._k):
digest = self._hash_fn.hash(item, i) % self.size
# check if the digest is in bit array
# if there is one 0 found in bit_array, then
# the item does not exists at all
if not self._bit_array[digest]:
return False
return True
After we have constructed the simple bloom filter class, we are now ready to test this out!
test_elements = [
'hello world',
'hello 1',
'hello3'
]
bf = SimpleBloomFilter(mmh3, len(test_elements), 0.01)
for el in test_elements:
bf.add(el)
for el in test_elements:
print('is `{}` exists in the filter? {}'.format(el, bf.is_possibly_exists(el)))
test1 = 'not exists'
print('is `{}` exists in the filter? {}'.format(test1, bf.is_possibly_exists(test1)))
is `hello world` exists in the filter? True
is `hello 1` exists in the filter? True
is `hello3` exists in the filter? True
is `not exists` exists in the filter? False
It turns out working like we are expecting! Hurray! Now we want to see how much space that we save for implementing the bloom filter
print('size of test elements: {} bytes'.format(sys.getsizeof(test_elements)))
print('size of bloom filters: {} bytes'.format(sys.getsizeof(bf)))
size of test elements: 88 bytes
size of bloom filters: 56 bytes
It doesn’t seems to be much of saving, eh? Let’s simulate it with larger elements!

import hashlib
def simulate_bloom_filter_size(element_size):
# generate larger test elements
test_elements = list()
test_element_length = element_size
bf = SimpleBloomFilter(mmh3, test_element_length, 0.01)
for i in range(test_element_length):
str_generator = hashlib.md5('{}'.format(i).encode())
el = str_generator.hexdigest()
test_elements.append(el)
return (sys.getsizeof(test_elements), sys.getsizeof(bf._bit_array), bf)
el_size = 10000
print('With {} Elements'.format(el_size))
print('------------------------------------------')
data_size, bf_size, _ = simulate_bloom_filter_size(el_size)
print('size of test elements: {:,} bytes'.format(data_size))
print('size of bloom filters: {:,} bytes'.format(bf_size))
With 10000 Elements
------------------------------------------
size of test elements: 87,624 bytes
size of bloom filters: 96 bytes

Okay we got this, but we want to know more! what if we extends until 100000?
import numpy as np
import matplotlib.pyplot as plt
observation_len = 50
c = np.linspace(1, 100000, observation_len)
data_sizes = list()
bf_sizes = list()
for el_size in c:
data_size, bf_size, bf = simulate_bloom_filter_size(int(el_size))
data_sizes.append(data_size)
bf_sizes.append(bf_size)
f, ax = plt.subplots(figsize=(11, 9))
plt.title('Data vs Bloom Filter Size in Bytes')
plt.plot(np.arange(observation_len), data_sizes, label='Data Size')
plt.plot(np.arange(observation_len), bf_sizes, label='Bloom Filter Size')
plt.legend()
plt.show()
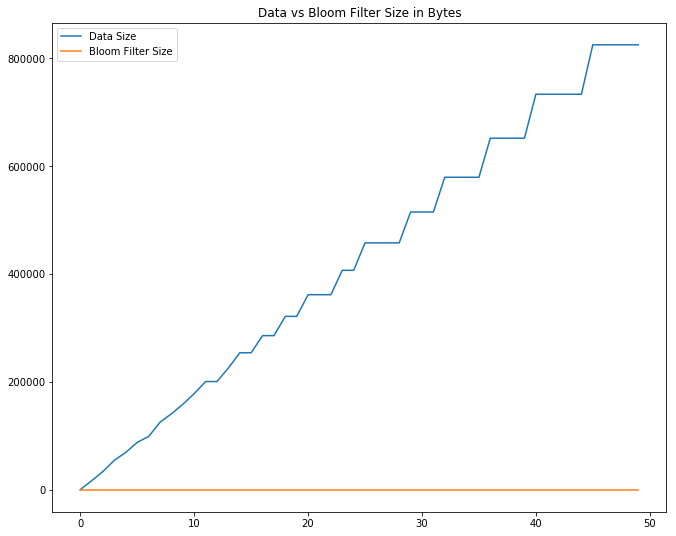
print('largest data size: {:,} bytes'.format(data_sizes[-1]))
print('largest bloom filter size: {:,} bytes'.format(bf_sizes[-1]))
largest data size: 824,464 bytes
largest bloom filter size: 96 bytes
Conclusion
Bloom Filter is awsome! (if you have matched the condition to use it!)

References
- https://en.wikipedia.org/wiki/Bloom_filter
- https://stackoverflow.com/questions/11669178/how-to-create-an-array-of-bits-in-python
- https://www.geeksforgeeks.org/bloom-filters-introduction-and-python-implementation/
- https://stackoverflow.com/questions/449560/how-do-i-determine-the-size-of-an-object-in-python