Deep Learning - Week 4 Lecture Notes
What is Deep Neural Network?
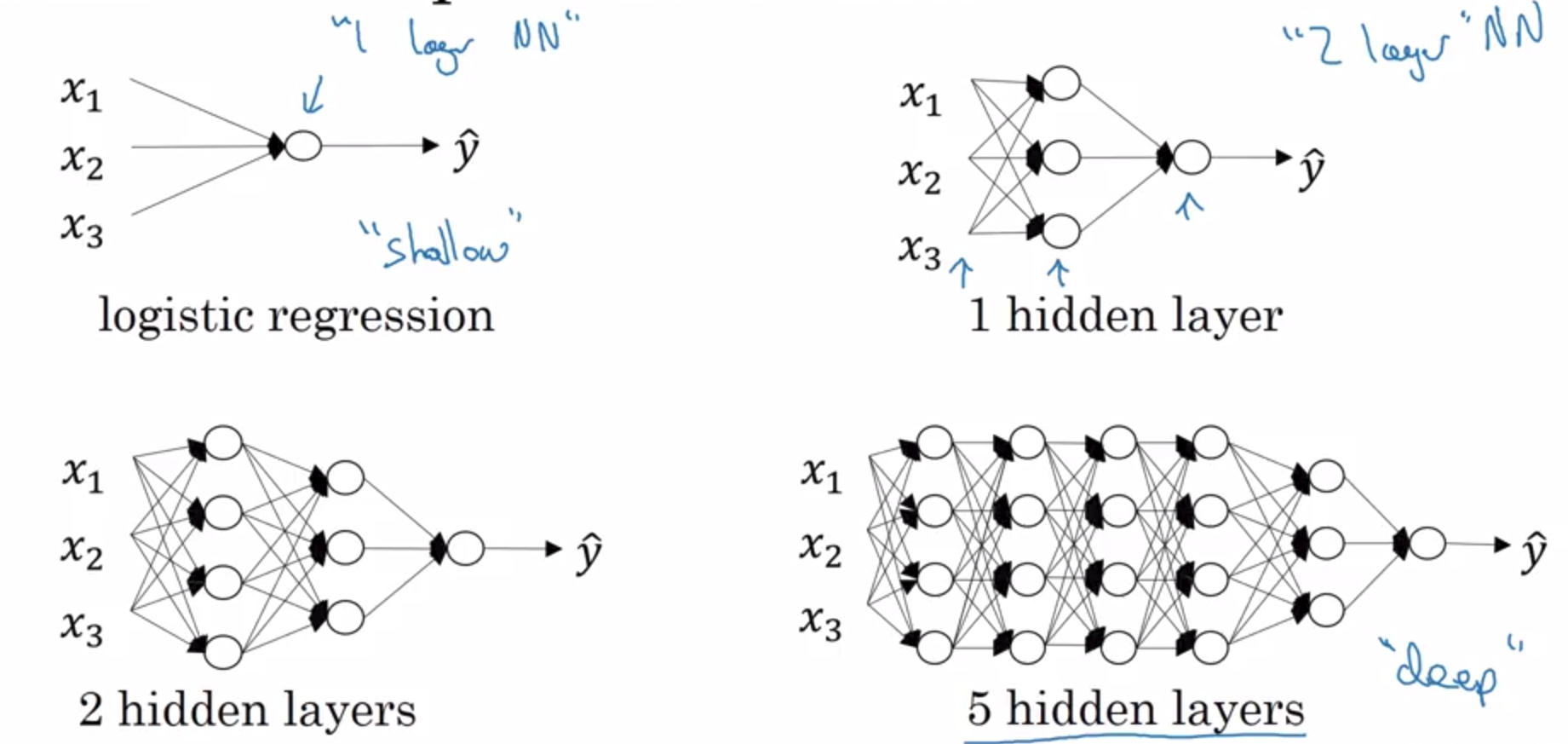
as you can see, from the past 3 courses we have explored logistic regression as a shallow network.
Notations
| Notation | Description |
|---|---|
| $l$ | number of layers |
| $n$ | number of hidden units |
| $n^{[l}$ | number of hidden units at layer $l$ |
| $a^{[l]}$ | activations in layer $l$ |
| $a^{[l]} = g^{[l]}(z^{[l]})$ | activations in layer $l$ |
| $W^{[l]}$ | weights in layer $l$ for $z^{[l]}$ |
Forward Propagation in Deep Network
basically same from before, lol

Getting your Matrix Dimension Right
to sum up:
| Variable | Shape / Dimension |
|---|---|
| $w^{[l]}$ | $(n^{[l]}, n^{[l-1]})$ |
| $b^{[l]}$ | $(n^{[l]}, 1)$ |
| $dw^{[l]}$ | $(n^{[l]}, n^{[l-1]})$ |
| $db^{[l]}$ | $(n^{[l]}, 1)$ |
Additional notes:
dimension of $z^{[l]}$ should be same as $a^{[l]}$
Why Deep Neural Networks Works?
Circuit theory
There are functions you can compute with a “small” L-layer deep neural network that shallower networks require exponentially more hidden units to compute
means: if we try to compute a function $ \hat y $ with depth $ n $, and try to compute the same function with shallower network say with depth $ n - x$, we might ended up need to add exponentially more hidden units (not layers), for example we might have to add $2^{x}$ more units to the current.
Deep learning is just branding!

Start with logistic regression, then 1 hidden layer, then 2 hidden layer first!