How to Do Conjoint Analysis in python
This post shows how to do conjoint analysis using python. Conjoint analysis is a method to find the most prefered settings of a product [11].
Usual fields of usage [3]:
- Marketing
- Product management
- Operation Research
For example:
- testing customer acceptance of new product design.
- assessing appeal of advertisements and service design.
import pandas as pd
import numpy as np
Here we used Immigrant conjoint data described by [6]. It consists of 2 possible conjoint methods: choice-based conjoint (with selected column as target variable) and rating-based conjoint (with rating as target variable).
Preparing The Data
# taken from imigrant conjoint data
df = pd.read_csv('https://dataverse.harvard.edu/api/access/datafile/2445996?format=tab&gbrecs=true', delimiter='\t')
df.head()
| resID | atmilitary | atreligion | ated | atprof | atinc | atrace | atage | atmale | selected | rating | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 383 | 1 | 6 | 3 | 6 | 6 | 1 | 6 | 2 | 0 | 0.333333 |
| 1 | 383 | 2 | 1 | 1 | 4 | 3 | 6 | 4 | 1 | 1 | 0.500000 |
| 2 | 383 | 1 | 3 | 5 | 5 | 1 | 2 | 5 | 2 | 1 | 0.666667 |
| 3 | 383 | 2 | 4 | 5 | 3 | 2 | 1 | 6 | 1 | 0 | 0.666667 |
| 4 | 383 | 2 | 1 | 2 | 3 | 6 | 2 | 2 | 2 | 0 | 0.333333 |
# checking for empty data
df.isnull().sum()
resID 0
atmilitary 0
atreligion 0
ated 0
atprof 0
atinc 0
atrace 0
atage 0
atmale 0
selected 0
rating 10
dtype: int64
# remove empty data
clean_df = df[~df.rating.isnull()]
Doing The Conjoint Analysis
y = clean_df['selected']
x = clean_df[[x for x in df.columns if x != 'selected' and x != 'resID' and x != 'rating']]
xdum = pd.get_dummies(x, columns=[c for c in x.columns if c != 'selected'])
xdum.head()
| atmilitary_1 | atmilitary_2 | atreligion_1 | atreligion_2 | atreligion_3 | atreligion_4 | atreligion_5 | atreligion_6 | ated_1 | ated_2 | ... | atrace_5 | atrace_6 | atage_1 | atage_2 | atage_3 | atage_4 | atage_5 | atage_6 | atmale_1 | atmale_2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ... | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
5 rows × 40 columns
[11] has complete definition of important attributes in Conjoint Analysis
Utility of an alternative $U(x)$ is
\[U(x) = \sum_{i=1}^{m}\sum_{j=1}^{k_{i}}u_{ij}x_{ij}\]where:
$u_{ij}$: part-worth contribution (utility of jth level of ith attribute)
$k_{i}$: number of levels for attribute i
$m$: number of attributes
Importance of an attribute $R_{i}$ is defined as \(R_{i} = max(u_{ij}) - min(u_{ik})\) $R_{i}$ is the $i$-th attribute
Relative Importance of an attribute $Rimp_{i}$ is defined as \(Rimp_{i} = \frac{R_{i}}{\sum_{i=1}^{m}{R_{i}}}\)
Essentially conjoint analysis (traditional conjoint analysis) is doing linear regression where the target variable could be binary (choice-based conjoint analysis), or 1-7 likert scale (rating conjoint analysis), or ranking(rank-based conjoint analysis).
import statsmodels.api as sm
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use('bmh')
res = sm.OLS(y, xdum, family=sm.families.Binomial()).fit()
res.summary()
| Dep. Variable: | selected | R-squared: | 0.091 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.083 |
| Method: | Least Squares | F-statistic: | 10.72 |
| Date: | Sun, 09 Dec 2018 | Prob (F-statistic): | 7.39e-51 |
| Time: | 15:49:37 | Log-Likelihood: | -2343.3 |
| No. Observations: | 3456 | AIC: | 4753. |
| Df Residuals: | 3423 | BIC: | 4956. |
| Df Model: | 32 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| atmilitary_1 | 0.0808 | 0.008 | 9.585 | 0.000 | 0.064 | 0.097 |
| atmilitary_2 | 0.1671 | 0.008 | 19.810 | 0.000 | 0.151 | 0.184 |
| atreligion_1 | 0.0931 | 0.018 | 5.132 | 0.000 | 0.058 | 0.129 |
| atreligion_2 | 0.0578 | 0.018 | 3.144 | 0.002 | 0.022 | 0.094 |
| atreligion_3 | 0.0803 | 0.018 | 4.411 | 0.000 | 0.045 | 0.116 |
| atreligion_4 | 0.0797 | 0.018 | 4.326 | 0.000 | 0.044 | 0.116 |
| atreligion_5 | -0.0218 | 0.018 | -1.185 | 0.236 | -0.058 | 0.014 |
| atreligion_6 | -0.0411 | 0.018 | -2.256 | 0.024 | -0.077 | -0.005 |
| ated_1 | -0.1124 | 0.018 | -6.115 | 0.000 | -0.148 | -0.076 |
| ated_2 | 0.0278 | 0.019 | 1.464 | 0.143 | -0.009 | 0.065 |
| ated_3 | 0.0366 | 0.019 | 1.942 | 0.052 | -0.000 | 0.074 |
| ated_4 | 0.0737 | 0.018 | 4.076 | 0.000 | 0.038 | 0.109 |
| ated_5 | 0.0649 | 0.018 | 3.570 | 0.000 | 0.029 | 0.101 |
| ated_6 | 0.1572 | 0.018 | 8.949 | 0.000 | 0.123 | 0.192 |
| atprof_1 | 0.1084 | 0.018 | 5.930 | 0.000 | 0.073 | 0.144 |
| atprof_2 | 0.0852 | 0.019 | 4.597 | 0.000 | 0.049 | 0.122 |
| atprof_3 | 0.0910 | 0.018 | 5.060 | 0.000 | 0.056 | 0.126 |
| atprof_4 | 0.0674 | 0.018 | 3.716 | 0.000 | 0.032 | 0.103 |
| atprof_5 | 0.0145 | 0.019 | 0.779 | 0.436 | -0.022 | 0.051 |
| atprof_6 | -0.1186 | 0.018 | -6.465 | 0.000 | -0.155 | -0.083 |
| atinc_1 | 0.0081 | 0.018 | 0.448 | 0.654 | -0.027 | 0.043 |
| atinc_2 | 0.0316 | 0.019 | 1.662 | 0.097 | -0.006 | 0.069 |
| atinc_3 | 0.0716 | 0.018 | 4.020 | 0.000 | 0.037 | 0.106 |
| atinc_4 | 0.0397 | 0.018 | 2.154 | 0.031 | 0.004 | 0.076 |
| atinc_5 | 0.0808 | 0.018 | 4.451 | 0.000 | 0.045 | 0.116 |
| atinc_6 | 0.0161 | 0.018 | 0.872 | 0.383 | -0.020 | 0.052 |
| atrace_1 | 0.0274 | 0.018 | 1.494 | 0.135 | -0.009 | 0.063 |
| atrace_2 | 0.0527 | 0.018 | 2.881 | 0.004 | 0.017 | 0.089 |
| atrace_3 | 0.0633 | 0.018 | 3.556 | 0.000 | 0.028 | 0.098 |
| atrace_4 | 0.0037 | 0.019 | 0.198 | 0.843 | -0.033 | 0.040 |
| atrace_5 | 0.0324 | 0.018 | 1.787 | 0.074 | -0.003 | 0.068 |
| atrace_6 | 0.0683 | 0.019 | 3.687 | 0.000 | 0.032 | 0.105 |
| atage_1 | 0.0680 | 0.018 | 3.770 | 0.000 | 0.033 | 0.103 |
| atage_2 | 0.0934 | 0.019 | 4.957 | 0.000 | 0.056 | 0.130 |
| atage_3 | 0.0900 | 0.018 | 4.967 | 0.000 | 0.054 | 0.125 |
| atage_4 | 0.0711 | 0.019 | 3.837 | 0.000 | 0.035 | 0.107 |
| atage_5 | 0.0038 | 0.018 | 0.208 | 0.835 | -0.032 | 0.039 |
| atage_6 | -0.0783 | 0.018 | -4.276 | 0.000 | -0.114 | -0.042 |
| atmale_1 | 0.1228 | 0.008 | 14.616 | 0.000 | 0.106 | 0.139 |
| atmale_2 | 0.1250 | 0.008 | 14.787 | 0.000 | 0.108 | 0.142 |
| Omnibus: | 0.070 | Durbin-Watson: | 2.872 |
|---|---|---|---|
| Prob(Omnibus): | 0.966 | Jarque-Bera (JB): | 391.306 |
| Skew: | -0.011 | Prob(JB): | 1.07e-85 |
| Kurtosis: | 1.352 | Cond. No. | 1.27e+16 |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 4.28e-29. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
df_res = pd.DataFrame({
'param_name': res.params.keys()
, 'param_w': res.params.values
, 'pval': res.pvalues
})
# adding field for absolute of parameters
df_res['abs_param_w'] = np.abs(df_res['param_w'])
# marking field is significant under 95% confidence interval
df_res['is_sig_95'] = (df_res['pval'] < 0.05)
# constructing color naming for each param
df_res['c'] = ['blue' if x else 'red' for x in df_res['is_sig_95']]
# make it sorted by abs of parameter value
df_res = df_res.sort_values(by='abs_param_w', ascending=True)
f, ax = plt.subplots(figsize=(14, 8))
plt.title('Part Worth')
pwu = df_res['param_w']
xbar = np.arange(len(pwu))
plt.barh(xbar, pwu, color=df_res['c'])
plt.yticks(xbar, labels=df_res['param_name'])
plt.show()
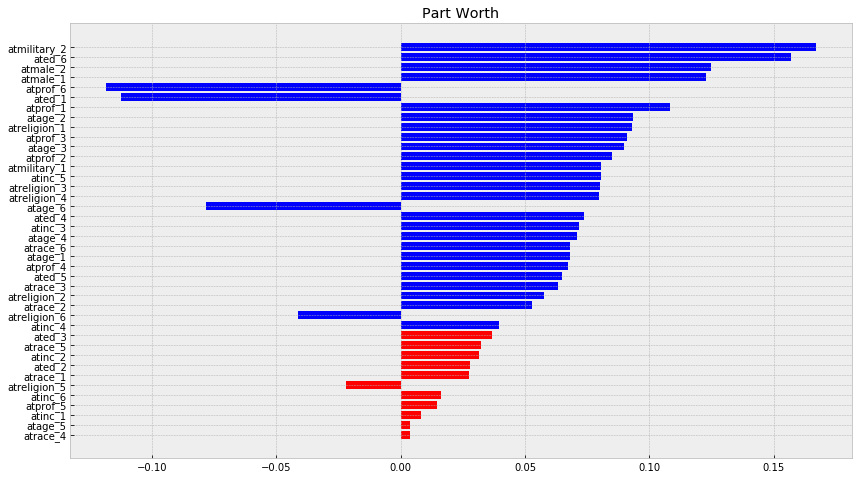
Now we will compute importance of every attributes, with definition from before, where:
\[R_{i} = max(u_{ij}) - min(u_{ik})\] \[Rimp_{i} = \frac{R_{i}}{\sum_{i=1}^{m}{R_{i}}}\]sum of importance on attributes will approximately equal to the target variable scale: if it is choice-based then it will equal to 1, if it is likert scale 1-7 it will equal to 7. In this case, importance of an attribute will equal with relative importance of an attribute because it is choice-based conjoint analysis (the target variable is binary).
# need to assemble per attribute for every level of that attribute in dicionary
range_per_feature = dict()
for key, coeff in res.params.items():
sk = key.split('_')
feature = sk[0]
if len(sk) == 1:
feature = key
if feature not in range_per_feature:
range_per_feature[feature] = list()
range_per_feature[feature].append(coeff)
# importance per feature is range of coef in a feature
# while range is simply max(x) - min(x)
importance_per_feature = {
k: max(v) - min(v) for k, v in range_per_feature.items()
}
# compute relative importance per feature
# or normalized feature importance by dividing
# sum of importance for all features
total_feature_importance = sum(importance_per_feature.values())
relative_importance_per_feature = {
k: 100 * round(v/total_feature_importance, 3) for k, v in importance_per_feature.items()
}
alt_data = pd.DataFrame(
list(importance_per_feature.items()),
columns=['attr', 'importance']
).sort_values(by='importance', ascending=False)
f, ax = plt.subplots(figsize=(12, 8))
xbar = np.arange(len(alt_data['attr']))
plt.title('Importance')
plt.barh(xbar, alt_data['importance'])
for i, v in enumerate(alt_data['importance']):
ax.text(v , i + .25, '{:.2f}'.format(v))
plt.ylabel('attributes')
plt.xlabel('% importance')
plt.yticks(xbar, alt_data['attr'])
plt.show()
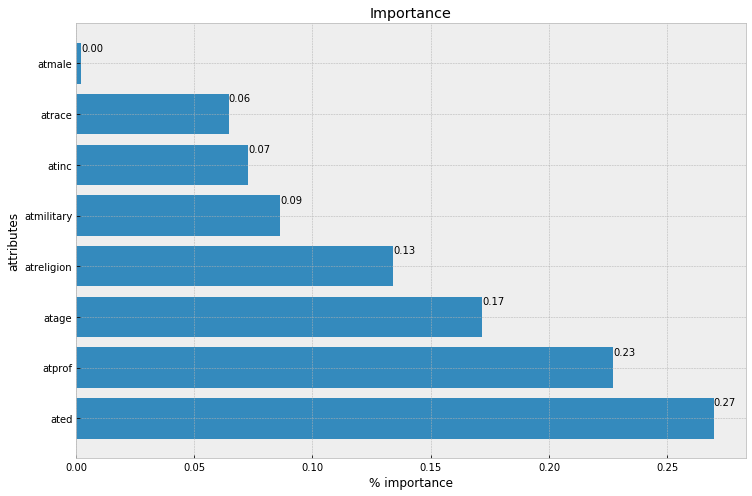
alt_data = pd.DataFrame(
list(relative_importance_per_feature.items()),
columns=['attr', 'relative_importance (pct)']
).sort_values(by='relative_importance (pct)', ascending=False)
f, ax = plt.subplots(figsize=(12, 8))
xbar = np.arange(len(alt_data['attr']))
plt.title('Relative importance / Normalized importance')
plt.barh(xbar, alt_data['relative_importance (pct)'])
for i, v in enumerate(alt_data['relative_importance (pct)']):
ax.text(v , i + .25, '{:.2f}%'.format(v))
plt.ylabel('attributes')
plt.xlabel('% relative importance')
plt.yticks(xbar, alt_data['attr'])
plt.show()
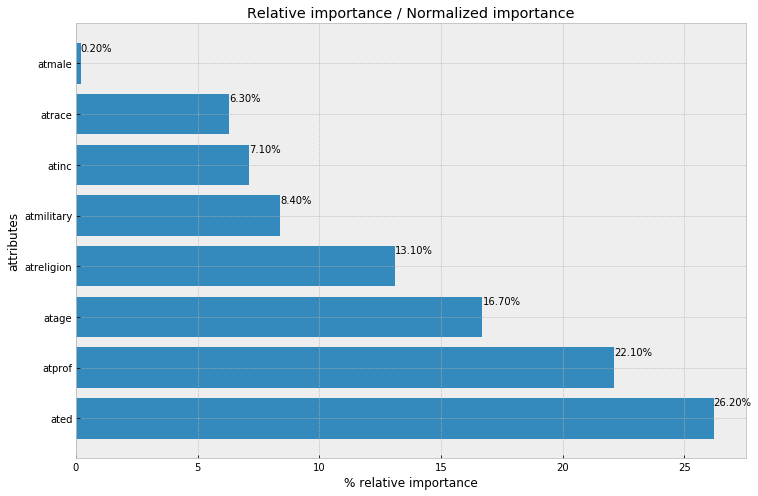
References
[3] Conjoint Analysis Wikipedia
[4] Conjoint Analysis - Towards Data Science Medium
[8] Traditional Conjoin Analysis - Jupyter Notebook
[9] Business Research Method - 2nd Edition - Chap 19
[10] Tentang Data - Conjoint Analysis Part 1 (Bahasa Indonesia)
[11] Business Research Method, 2nd Edition, Chapter 19 (Safari Book Online)